1.2.3 Systèmes complexes et chaos

La crédibilité d'une science naît de sa faculté à relier les causes et les effets, et, de là, à rendre les phénomènes prédictibles. Or, certains systèmes manifestent des comportements aléatoires qui semblent défier la connaissance par leur complexité et leur imprévisibilité: citons par exemple les turbulences, la météorologie, la fluctuation des populations, les embouteillages routiers, les arythmies létales ou les accidents vasculaires. Ces systèmes échappent à toute analyse selon la méthodologie classique, qui consiste à rechercher une cause individuelle à tout événement en le décomposant en ses éléments les plus simples. La conception mathématique linéaire, qui décrit des effets directement proportionnés à l’intensité de leur cause, n’a plus cours dans ces modèles non-linéaires où elle ne voit que du chaos [8,10]. Les systèmes non-linéaires sont caractérisés par une variabilité d’effets qui paraît imprévisible: des causes minuscules peuvent y engendrer des résultats gigantesques et inattendus. Ils sont également caractérisés par un comportement global différent de celui des éléments qui le constituent ; un système complexe peut passer certains seuils, et donner naissance à des propriétés émergentes différentes des propriétés initiales du système ; une propriété émergente est une caractéristique imprévisible au niveau local qui apparaît au niveau global [22]. Les systèmes non-linéaires sont aussi extrêmement dépendants des conditions initiales définies comme celles du temps zéro de l'observation. Sur l’échelle du temps, ils tendent à maintenir une variabilité adaptatrice mais non à préserver leur stabilité [3]. Enfin, les équations qui décrivent ces systèmes non-linéaires n’ont en général pas de solution analytique [7] ; seule la simulation informatique permet d’élucider les comportements possibles du système. 
 

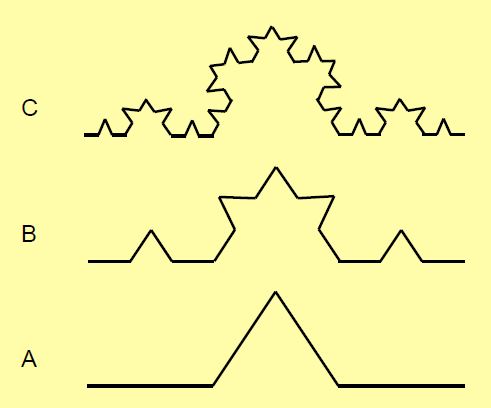
Cette nouvelle méthodologie a dévoilé que ces comportements apparemment chaotiques sont régis par des structures géométriques élégantes qui engendrent de l'aléatoire, et ceci dès que le système examiné comporte trois ou plus degrés de liberté (ou variables indépendantes) et que celles-ci, en tout ou en partie, suivent des progressions géométriques exponentielles [4]. Un exemple simple est un pendule métallique oscillant entre trois aimants équidistants ; celui-ci va s’immobiliser au-dessus d’un des aimants après avoir parcouru un mouvement compliqué et désordonné que l’on ne pourrait prévoir que si l’on pouvait connaître avec une exactitude infinie le champ d’attraction de chaque aimant et la position initiale exacte du pendule, ce qui est évidemment impossible puisque la précision des mesures est limitée et puisque le temps zéro de l'expérience n'est pas le temps zéro de l'univers: on intercepte un phénomène toujours déjà en cours [22]. Les systèmes complexes n’ont nullement besoin d’être compliqués pour donner lieu à d’innombrables possibilités au milieu desquelles ils évoluent de manière surprenante. Si l’on ajoute quelques grains à un tas de sable, la hauteur de celui-ci augmente, de même que sa pente ; cette pente croît jusqu’à un certain seuil, au-delà duquel se déclenche une avalanche. Si l’on recommence continuellement l’opération, on verra que la taille des avalanches est indépendante de la quantité de sable ajoutée, et que leur fréquence est inversement proportionnelle au logarithme de leur taille [22]. Finalement, la notion de fractale est fréquemment associée à la complexité et au chaos ; la fractale est un concept géométrique décrivant un objet composé de sous-unités dont la structure est similaire à celle de l’ensemble (Figure 1.6 et Figure 1.7) [3,9]. Ces quelques points méritent un développement un peu plus détaillé en relation avec la biologie.
 

Figure 1.6: Construction de fractales (courbe de Koch). Le tiers central d’une droite (A, en bas) est transformé en un triangle isocèle dont le côté est égal à la longueur du tiers de la droite primitive. Cette opération est répétée sur les quatre segments de cette droite (B). Elle est répétée une deuxième fois pour obtenir l’image du haut (C). On peut réitérer cette opération autant de fois que l’on veut : la longueur totale de la courbe obtenue tend vers l’infini alors que ses extrémités sont les mêmes que celles du segment d’origine et qu’elle ne s’élève pas plus haut. Pour obtenir la longueur d’un côté, il faut diviser la longueur de la courbe primitive par 4 et multiplier le résultat par 3 (voir courbe A). La puissance de 3 égale à 4 est 1.2619 (3^1.2619) [8]. La dimension fractale de la courbe est 1.2619. La dimension d’une fractale est toujours située entre 1 et 2. La dimension fractale de la côte de Norvège avec ses fjords enchevêtrés, par exemple, est 1.52. Dans la réalité, la longueur mesurée est fonction de l’échelle choisie. Si la carte représentant la côte de Norvège est couverte d’une grille de petits carrés et que l’on mesure la longueur de la côte dans chaque carré, la longueur totale sera d’autant plus grande que les carrés choisis seront plus petits. Un graphique mettant en regard le logarithme de la longueur de côte mesurée dans chaque carré (en ordonnée) et le logarithme de la taille des carrés (en abscisse) montre que la relation est une droite dont la pente est la dimension fractale (voir Figure 1.8). Le produit des logarithmes de la longueur de côte et de la taille du carré est une constante : on dit qu’il y a invariance d’échelle.
 

 

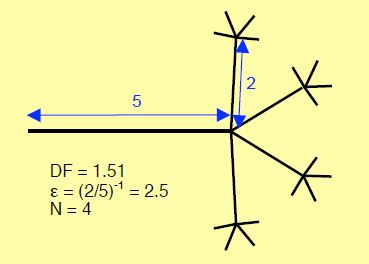
Figure 1.7: Embranchement fractal théorique illustrant de manière schématique un réseau de dendrites, des capillaires coronariens ou des subdivisions de fibres de Purkinje. En l’occurrence, la dimension fractale (DF) est 1.51, l’échelle liant la taille des branches (ε) est (2/5)^-1 ou 2.5 et le nombre d’embranchements (N) est 4. Calcul de la dimension fractale : DF = log 4/log (5/2) = 1.51) [3].
 

Des marins ont depuis des siècles décrit l’apparition soudaine d’une vague monstrueuse au cours de gros temps ; certains ont sanci, beaucoup ont coulé et quelques-uns en sont revenus. Cette vague scélérate a été tenue pour une légende parce qu’elle paraît exceptionnelle et que, décidément, les marins boivent beaucoup. Mais dans la deuxième moitié du XXème siècle, quelques cargos ou pétroliers ont eu le temps de lancer un SOS avant de disparaître corps et biens, décrivant se trouver en face d’un mur d’eau gigantesque qui allait les engloutir. C’est lorsqu’on eut l’idée de modéliser la dynamique des vagues océaniques sur ordinateur et de faire tourner le programme pour créer des milliards de milliards de vagues qu’on s’aperçut que, sporadiquement, apparaissait un véritable monstre de 25 mètres de hauteur. Ce que les observations satellite ont pu confirmer. Les petites vagues sont fréquentes, les grandes sont plus rares, et les monumentales sont exceptionnelles. Il en est de même des tremblements de terre : leur magnitude sur l’échelle de Richter (qui est logarithmique) est directement liée au logarithme de leur fréquence ; la relation est une droite dont la pente est une dimension fractale (explication aux Figures 1.6, 1.7 et 1.8). Il n’existe aucune différence de nature ou de cause entre un gros tremblement de terre et un petit, ou entre une vague immense et un clapot : seule l’intensité diffère. Les évènements les plus importants sont simplement plus rares. Il n’est nul besoin d’un déclencheur spectaculaire pour provoquer une catastrophe. En mathématique, la fréquence d’un événement est égale à 1 divisé par une certaine puissance définissant l’importance de cet évènement. En d’autres termes, la taille d’un événement est égale à 1 divisé par sa fréquence (f) élevée à une certaine puissance (P) représentant cette taille : 1/f^P. Chez les mammifères, l'augmentation de la fréquence cardiaque (f) par rapport à la diminution de la masse corporelle (M) est elle aussi une ligne droite sur une échelle logarithmique (où f = 241 M^-0.25) (Figure 1.8) [20,21]. C’est la même relation qui existe entre l’importance des tremblements de terre et leur fréquence.
 

 

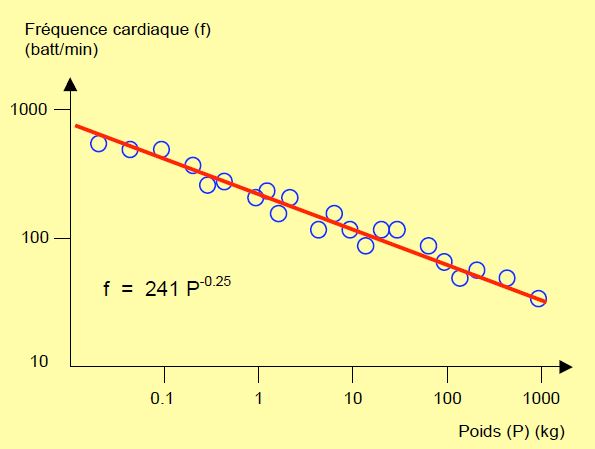
Figure 1.8: Relation entre le poids des mammifères et leur fréquence cardiaque. La fréquence est d’autant plus élevée que l’animal est petit. L’échelle est logarithmique pour les deux données [d'après Schmidt-Nielsen K. Animal physiology. 5th edition. Cambridge: Cambridge University Press, 2002, p 101]. On obtient le même type de droite dans d’autres lois de puissance, comme la relation entre la puissance des tremblements de terre ou la hauteur des vagues et leur fréquence, la relation entre la quantité d’ADN contenu dans une cellule et le nombre de types cellulaires différents que possède l’être vivant considéré, ou la relation entre l’échelle de la carte de géographie et la longueur de la côte. Dans ce dernier cas, la pente de la droite (sa puissance) est la mesure de la dimension fractale de la côte.
 

Le génome humain comprend entre 30'000 et 100'000 gènes qui peuvent agir les uns sur les autres en s’activant ou se désactivant mutuellement (cross-talk) dans un réseau complexe de connexions et de rétrocontrôles (feed-back) ; ces gènes contrôlent la différentiation et l’activité cellulaire de notre organisme. Or nous avons 256 variétés de cellules dans notre corps. En comparant les espèces de la bactérie à l’homme, on voit que le nombre de variétés cellulaires croît en fonction de la racine carrée du nombre de gènes [11]. Autrement dit, les règles qui valent pour les vagues, les séismes et les tas de sable s’appliquent aussi aux gènes, aux cellules et aux organes de notre corps. Il y a bien invariance d’échelle ; nous sommes dans un système fractal. 
 

Cette loi de puissance (1/f^P) concerne toujours des systèmes complexes formés de nombreux composants, systèmes ouverts alimentés par une source d’énergie externe qui se gèrent spontanément dans un état critique auto-organisé situé à la frontière entre la stabilité et le chaos, et qui s’y maintiennent dans un équilibre dynamique et instable [10]. Un bon exemple est le système du réseau, ensemble de points partiellement reliés deux à deux et constitués de multiples éléments interdépendants. Dans le cerveau, ces éléments sont des neurones reliés par leurs dendrites, dans la cellule ce sont des molécules reliées par des réactions chimiques, et dans la société ce sont des individus liés par leurs relations sociales. Mais dans chacun de ces systèmes, la probabilité pour qu’un élément « e » soit relié à k autres éléments est aussi une loi de puissance : 1/k^e. Le réseau peut adopter un comportement régulier ou aléatoire selon le nombre d’interconnections et le nombre d’éléments, mais lorsque ce nombre est suffisamment grand, le réseau est en équilibre dynamique autour d’une position proche de la transition entre l’ordre et le chaos [11]. Il présente alors une certaine robustesse contre les perturbations ou les ruptures de connexions, mais fait aussi preuve d’une imprévisibilité fondamentale. En effet, le nombre de combinaisons possibles devient vite astronomique, même dans un réseau de petite taille : avec mille éléments interconnectés pouvant être chacun dans 2 états (activé ou désactivé, par exemple), on obtient 10³⁰⁰ configurations possibles [22] ; ce nombre est tel que l’âge de l’Univers serait un temps insuffisant à un ordinateur surpuissant pour calculer toutes les combinaisons possibles. 
 

Mais il se passe un autre phénomène dans les systèmes complexes et les réseaux. Certaines combinaisons et certains circuits reviennent plus souvent que d'autres. Dans les réseaux, les liens se condensent autour de certains foyers (hubs) qui centralisent un maximum d'interconnexions et dont la fonction est prioritaire pour la circulation des informations (Figure 1.9) [13]. Un phénomène physiopathologique est un foyer d'intersections qui nous apparaît comme une entité autonome parce que nous simplifions la réalité pour nous la rendre compréhensible et manipulable; ce faisant, nous négligeons l'aspect réticulaire du réel et nous oublions que chaque élément est en totale interdépendance avec ceux auxquels il est relié au sein des réseaux. Sa description correspond en fait à isoler le hub et à analyser son fonctionnement indépendamment de ses multiples connexions. 
 

 

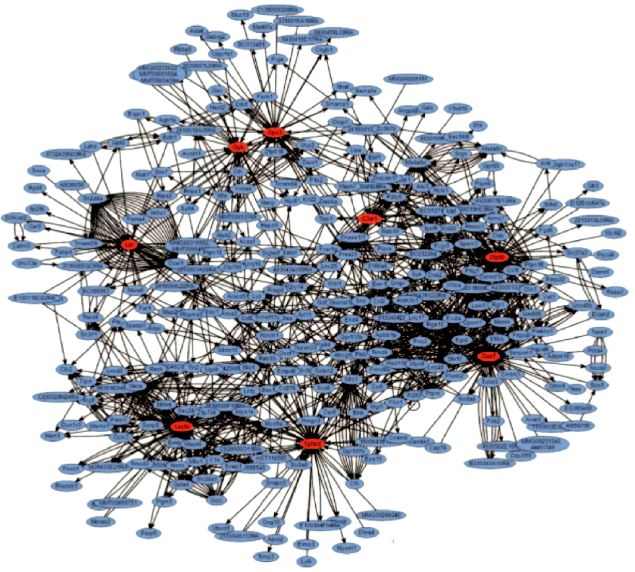
Figure 1.9: Image de réseaux contribuant à l'adiposité génétique chez la souris. Les hubs sont les 8 foyers rouges représentant chacun un des gènes impliqués dans la maladie [Lusis AJ, Weiss JN. Cardiovascular networks. Systems-based approaches to cardiovascular disease. Circulation 2010; 121:157-70].
 

Si nous simulons nos 30'000 gènes connus et leurs interconnexions dans un programme où chaque gène peut être activé ou inhibé, nous obtenons 10^9’000 combinaisons possibles. Ce chiffre est évidemment irréalisable. Or en faisant tourner un programme informatique de simulation, on voit que les innombrables possibilités se condensent autour d’un nombre restreint de réalisations ou d’états cycliques, en l’occurrence 173. Ces foyers de réalisations ont été appelés attracteurs ; leur nombre est équivalent à la racine carrée du nombre d’éléments (dans ce cas les gènes) [10,17]. Comme nous possédons entre 30'000 et 100'000 gènes, il est intrigant de constater que nous avons 256 espèces de cellules différentes, soit le nombre probable d’attracteurs correspondant à la racine carrée du nombre de gènes [10,22]. Au niveau global, la complexité engendre trop de possibilités pour être prévisible, mais apparaît profondément auto-organisée. 
 

Les rythmes physiologiques comme le rythme cardiaque, la respiration ou la pression artérielle ne sont pas strictement périodiques mais présentent des variations non-linéaires constantes que l’on peut partiellement assimiler à des fractales déroulées dans le temps au lieu de l’espace [7]. L’anarchie d’une arythmie ou l’hyper-régularité par perte des fluctuations conduisent toutes deux vers la pathologie [14]. Les fluctuations complexes du rythme cardiaque sont probablement une fonction physiologique essentielle assurant une meilleure robustesse du système face aux variations de l’environnement. L’EEG est un des signaux physiologiques les plus complexes. Les mathématiques non-linéaires sont mises à contribution en clinique pour analyser son tracé de différentes manières. L’entropie quantifie le degré d’aléatoire ou d’impredictibilité du signal (une onde sinusoïdale simple a une entropie de 0 alors qu’un bruit anarchique a une entropie maximale) ; la complexité normalisée quantifie le degré de répétition de séquences identiques dans un train de signal ; enfin la dimension fractale mesure l’augmentation de la disparité dans l’amplitude des signaux lorsque l’échantillonnage est de plus en plus espacé [6]. Toutes ces techniques sont utilisées pour l’analyse du tracé EEG et pour en extraire des informations sur la profondeur du sommeil.
 

Les théories mathématiques non-linéaires ont démontré que les limites de la prédictibilité sont inhérentes aux systèmes complexes pour deux raisons. En premier lieu, l'extrême sensibilité aux conditions initiales d'un système à interdépendances multiples conditionne son évolution et permet d'aboutir, par une cascade d'événements enchaînés dans le temps, à de vastes variations dans les résultats à long terme à partir de minuscules différences dans la situation de départ. Des phénomènes de dimensions inobservables à notre échelle prennent, par croissance exponentielle, des valeurs comparables aux grandeurs qui expriment l'état initial du système. Quelle que soit la précision des mesures de l’état initial, elle ne peut pas être infinie, donc un certain degré d’incertitude est toujours présent. Deuxièmement, la croissance de ces incertitudes y est exponentielle au fur et à mesure que le système évolue: toute mesure est entachée d'erreurs, et ces erreurs croissent si rapidement que toute prévision devient impossible. On a ainsi décrit un effet papillon: on peut calculer que le battement des ailes d'un papillon, événement minuscule s’il en est, a pour effet après quelque temps de modifier l'état de l'atmosphère terrestre et de sa météorologie de manière imprévisible [17]. En physique des fluides, il suffit d'un jour pour que des modifications sur des dimensions de l'ordre du centimètre soient transformées en changements de l'ordre de dix kilomètres [18]. Il existe ici une analogie intrigante avec le nadir de la performance myocardique qui survient 5-6 heures après une CEC [16] ou avec les complications cardiaques postopératoires dont l'incidence est maximale entre le 2ème et le 3ème jours postopératoires [12]. Peut-être sont-elles la conséquence d'une suite de modifications minuscules qui ont débuté en cours d'intervention mais qui ne peuvent pas encore être perçues par nos instruments de mesure à ce moment-là. Il existe aussi une analogie inquiétante avec la genèse des accidents : dans les systèmes complexes, des gestes en apparence anodins peuvent avoir des conséquences fâcheuses par amplification progressive. Il se peut même que ces gestes soient quotidiens, et qu’une fois, exceptionnellement, ils se retrouvent liés à une catastrophe parce que le hasard en a modifié le contexte.
 

On définit les conditions initiales comme celles du temps zéro de l'observation, mais le système est lui-même en constante évolution dans le temps: chaque instant représente les conditions initiales d'une autre séquence d'événements, lui-même héritier d'une situation précédente. De plus, un système complexe peut passer certains seuils, et donner naissance à des propriétés émergentes différentes des propriétés initiales du système; ainsi, en dessous d'une certaine température, l'eau cristallise, et la glace prend des caractéristiques non contenues dans la phase aqueuse ; c’est une transition de phase. Si l’on ajoute ou soustrait des grains de sable à un tas presque plat, les grains voisins ne sont pas modifiés et rien ne se passe. Mais dès lors que le tas est élevé et présente une pente assez raide, retirer ou ajouter un seul grain va déséquilibrer l’ensemble, et toute la pente va se modifier dans l’écroulement du tas. Accentuer la pente du tas de sable est l’équivalent d’une augmentation de l’interdépendance des grains, comme ajouter des connexions à un ensemble d’unités. Les systèmes assez compliqués pour donner naissance à des propriétés émergentes et tout de même assez stables pour être observés sont ceux dans lesquels chaque élément est relié à un ensemble de deux à cinq autres, et entretient avec eux des relations en feed-back qui peuvent être catalysatrices ou inhibitrices. Ce phénomène peut fournir une explication à l’origine de la vie. Dans la soupe primitive d’acides aminés d’où elle a démarré, il s’est établi un réseau de connexions entre substances chimiques réagissant les unes avec les autres ; certaines réactions étaient autocatalytiques et s’entretenaient, d’autres étaient inhibitrices et freinaient la formation de certaines molécules. Une hypothèse très plausible est que la vie représente une transition de phase dans un système chimique présentant un nombre suffisant de connexions en réseau. Quelques connexions en moins et rien ne se passe, quelques connexions en plus et la vie devient inévitable [10]. Celle-ci n’est peut-être pas un hasard, mais une nécessité. 
 

Comme une différence d'échelle introduit une différence de propriétés, la déconstruction d'un système complexe en unités plus simples que l'on additionne ne permet pas d'explorer le fonctionnement de l'ensemble lorsque des seuils organisationnels sont franchis. Un réseau interactif de neurones particulièrement dense peut amener une stimulation sensorielle à l'état de conscience au-dessus d'un certain seuil de complexité [19]. La variabilité individuelle s'efface à l'échelle collective, non pas par effet cumulatif d'un grand nombre d'unités différentes, mais bien parce qu'il se produit une homogénéisation progressive des entités les unes en fonction des autres; il émerge donc un comportement coopératif entre les unités individualisées [1]. D’où le titre d’un article fameux paru dans Science: "More is different" [2]. La variabilité individuelle n'est pas qu'un phénomène parasite perturbant le déterminisme préexistant. Elle est au contraire la source même de l'émergence de propriétés nouvelles agissant comme un noyau de cristallisation autour duquel l'ensemble peut se restructurer selon une nouvelle dimension par synergie plutôt que par accumulation. Ce type de paradigme paraît flou aux yeux de la physique mécanique classique, mais il est la base épistémologique de la biologie et de la neurophysiologie modernes.
 

Pour compliquer les résultats, les systèmes complexes sont dynamiques; les opérations s'y répètent sans cesse, telles les oscillations d'un pendule ou les battements du coeur. L'analyse mathématique de ces répétitions et de leur variabilité dévoile que ce sont les fluctuations d'importance minime qui dominent finalement le système tout entier, alors que ce système démontre la capacité de se rééquilibrer en permanence pour amortir l'effet des modifications grossières imposées par l'environnement [4]. Le concept du chaos remet en cause l'idée réductionniste qui consiste à analyser le comportement d'un système en le réduisant à celui des éléments qui le constituent; il impose la notion que son évolution à long terme est imprévisible, parce que la variabilité fait partie de sa nature. Le seul système capable de simuler un événement complexe dans ses moindres détails est cet événement lui-même. Dans le cadre de la prévisibilité du risque opératoire et des analyses de devenir des patients en anesthésie, ces concepts logiques éclairent sous un jour nouveau les difficultés rencontrées depuis vingt ans dans la recherche des déterminants du risque et des facteurs déclenchants de morbidité et de mortalité. Leur nature indéterministe et aléatoire exclut une prédictibilité individuelle fiable pour chaque malade. On comprend aussi que les résultats des essais cliniques randomisés et contrôlés, qui isolent certaines données à observer dans une population hautement sélectionnée, ne soient jamais confirmés avec autant de signification par les études faites dans le monde clinique réel où de multiples facteurs confondants interviennent en permanence.
 

On le sait en météorologie: quand bien même on connaîtrait tous les éléments en jeu à un instant précis, on ne pourrait faire des prédictions fiables qu'à court terme. Les systèmes dynamiques ou chaotiques peuvent s'étudier à deux niveaux: celui des trajectoires individuelles, qui sont l'illustration du désordre, et celui des ensembles, qui sont décrits par des distributions de probabilités et qui présentent à cette échelle un comportement analysable [15]. Une connaissance parfaite des facteurs en jeu dans l'ischémie myocardique ne permettrait donc qu'une prédiction probabiliste: il serait possible de définir l'appartenance d'un malade à une classe qui présente une probabilité définie de faire un infarctus, mais il reste impossible de savoir si ce malade particulier fera un infarctus ou non. La causalité n'étant pas linéaire mais multifactorielle et redondante, on ne peut prédire que des risques ou des chances par rapport à un ensemble d'individus. Le malade, lui, est au contraire dans un système binaire: il est vivant ou mort; il n'a que deux possibilités: 0% ou 100%. Inversement, le fait que ce malade particulier n'ait pas fait d'infarctus au cours d'une anesthésie ne change rien au risque inhérent à cette classe de patient et ne cautionne en rien la technique utilisée; la probabilité d'un évènement reste la même, que cet évènement se soit produit ou non. Un succès isolé ne prouve rien !
 

Il faut encore tenir compte d’un autre aspect des phénomènes. Dans les systèmes vivants, des erreurs et des incidents se produisent sans cesse, même si leurs effets sont estompés par les systèmes homéostasiques de l'organisme qui tendent à maintenir l'équilibre par rapport aux déviances. Tous ces systèmes comprennent de multiples contraintes qui peuvent se potentialiser ou s'annuler selon les circonstances. Ainsi le sort d'une plaque athéromateuse dépend de l'équilibre momentané des lipides et des cellules inflammatoires qu'elle contient, de sa capsule endothéliale, des facteurs déséquilibrants de l'instant (fumée, stress) ou des substances stabilisantes (statines par exemple), de l'activité des plaquettes et de la fibrinolyse, des forces de cisaillement locales (hypertension artérielle) et de l'activité endothéliale (anormale dans la maladie athéromateuse), de la diète et de la constitution génétique. Un thrombus peut être évacué par le débit, lysé rapidement, ou agrandi par hypercoagulabilité. La survie du myocarde distal dépend de ses besoins momentanés en O₂ (effort ou repos, tachycardie ou bradycardie, présence d’une valvulopathie), de l'apport en O₂ (hypoxie, hypotension, bas débit, anémie ou hyperviscosité) et du degré de collatéralisation. Si l’on scrute le niveau cellulaire, on voit par exemple que 1-2% des électrons cheminant dans la chaîne d’oxydo-réduction des mitochondries s'en échappe dans le cytoplasme et y forme des superoxides toxiques, en général lysés par des enzymes (super-O^--dismutases). Le DNA de chacune de nos cellules est quotidiennement l’objet de 10'000 de ces attaques oxydatives, dont certaines vont donner naissance à des mutations [5]; et ces dégâts s’accumulent avec l’âge. La survie de chacune de nos cellules est le fruit d’un équilibre dynamique entre les facteurs qui conditionnent sa croissance et ceux qui gèrent son apoptose. Cette dernière est programmée par des gènes, qui sont activés par le stress métabolique ou l’ischémie.
 

Cette énumération très partielle des multiples phénomènes en jeu simultanément traduit la non-prédictibilité fondamentale d'un événement, notamment lorsque celui-ci est aussi complexe et aussi variable qu’un accident d’avion ou un infarctus. Il est illusoire de vouloir le réduire à quelques causes simples, de le classer en catégories précises dont chacune aurait une thérapeutique propre, et de croire que l’importance de l’effet est proportionnel à celui de la cause. Face à cette diversité, nos traitements sont grossiers, mais ils fonctionnent dans une proportion significative de cas. On les considère comme adéquats simplement lorsque leur probabilité de tomber juste nous satisfait.
 

 

 

 

© CHASSOT PG  Avril 2007 Mise à jour Janvier 2012, Juillet 2017
 

Références